ADINAの新コネクタ要素による高度な構造解析モデリング

まえがき

複雑または、高度なソリッド要素モデルを、同等の機械的応答の構造要素に置き換えることが、しばしば要求されます。梁、トラス、バネ要素は、よく知られている例で、多くの状況で利用できます。しかし、様々な自由度で異なる非線形剛性や減衰応答のある、ブッシュ、ベアリング、ボールジョイント、一般的な形状の構造部品の応答は、より複雑になります。このような場合は、従来の構造要素では正確にモデル化できません。ADINAの新コネクタ要素は、ユーザーに上述のケースやその他の多くの便利ツールとして開発されました。

コネクタ要素は、線形または、非線形材料特性を持つ2節点の大変形の一般化バネ/ダンパ要素です。さらに、コネクタ要素は、剛体運動の場合、相対的な節点位置および向き（局所変位および回転）が変化しないままであり、要素の内部力が剛体運動に変換されるように、ユーザ定義変換のローカル座標系を持ちます。言い換えれば、モデル化された構造の応答は、剛体ボディの動きで保持されます。例えば、ショックアブソーバをモデリングするコネクタ要素は、その向きにかかわらず（その取り付けられたローカル座標系に対して）同じ応答になります。

モデリングケース

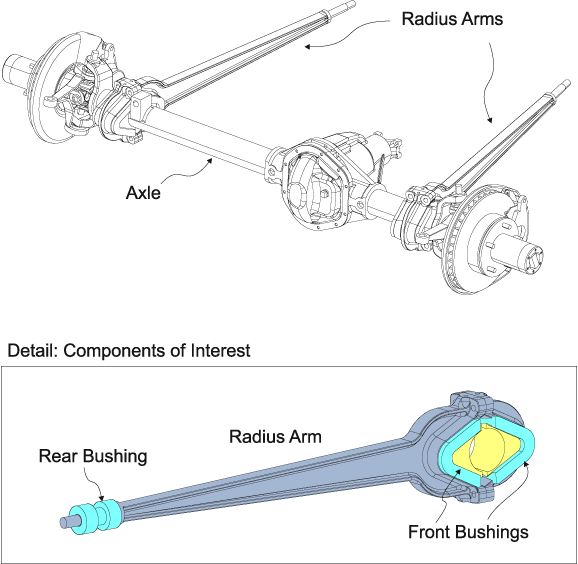
次の例は、軽量トラックサスペンション部品の3Dソリッド有限要素モデルが、接続ブッシュで完結したモデルの場合、計算コストのかからない同等の構造応答をする3つのコネクタ要素を使用してどのように置換えれるかを示しています。

図1は、車両のフロント車軸に関連して検討中の部品を示しています。図1の挿入図には、これらの部品の詳細があります。

ジョイントコネクタ要素

コネクタ要素を使用して、線形または、非線形のジョイント可動をモデル化でき、その6つの局所的自由度のそれぞれに対して個別の任意応答を用いることができます。要素の節点は、最初に分離されていても、一致していてもよく、ユーザは要素のローカル座標系と未変形状態を任意に定義することができます。

図2は、リアゴムブッシュとスチールシャフト接続の断面図を示しています。接続部が相対的に大きな平行移動および回転を受けると、ゴムブッシングは大きな歪みを受けます。また、鉄とゴム材の両方が高い体積弾性率を有するため、鋼製シャフトは適度な曲げを受ける。この相互作用をモデル化することにより、ジョイントの正確な応答を得ることが可能です。

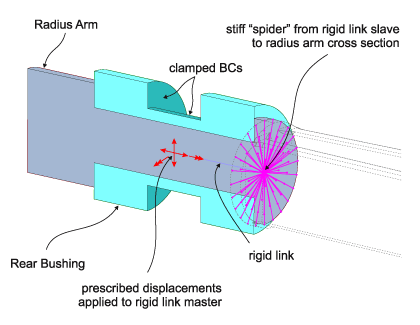
所定の変位および回転のセットが与えられると、対応する一組の反力およびモーメントを3Dソリッド有限要素 モデルから得ることができる。これらの変位と応答を利用して、6つの局所自由度のそれぞれにおける等価なコネクタ要素の非線形の力 - 変位の応答を定義することができます。（図3の上側）は、規定された平行移動および回転の下で明瞭に表現されるように、リアブッシュ/ラジアスアーム接続を示します。同等のコネクタ要素が示されており（図3の下側）、同じ規定された平行移動および回転を受けます。

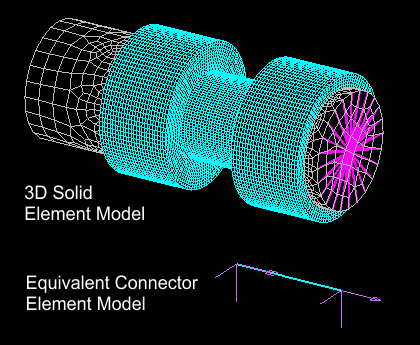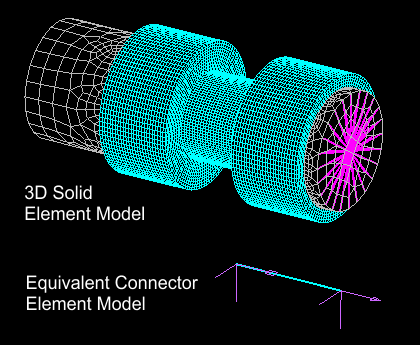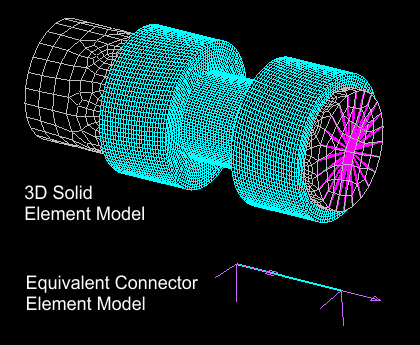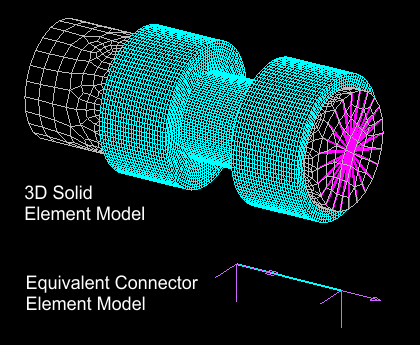
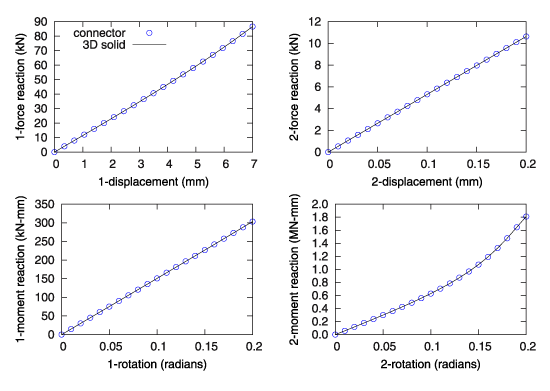
図4は3Dソリッドモデルとコネクタ要素モデルの応答の比較を示しています。 図から判るように、3Dソリッドモデルとコネクタ要素の応答は同じです。 フロントブッシュに対する応答も同様に得られます。

マトリクスコネクタ要素

コネクター要素はまた、ユーザーが構造体のローカル座標系（いくつかの方法でユーザーが指定できます）に対 する構造体の剛性行列を直接指定することもできます。コネクタ要素は、空間内を移動するときの向きや位置（コネクタ要素は常に大変位/大回転要素）に対して同じ応答（付属の座標系に対して）を提供します。

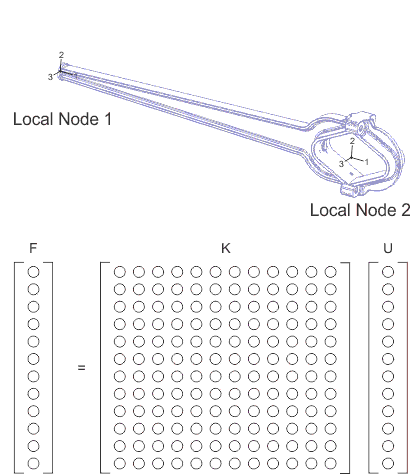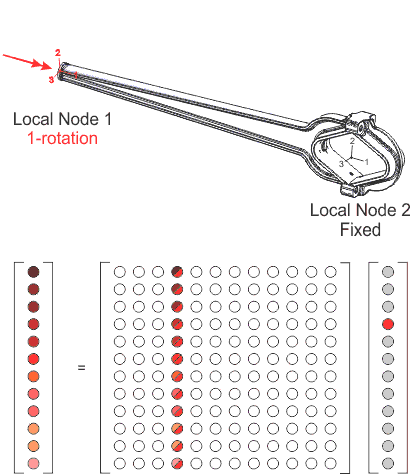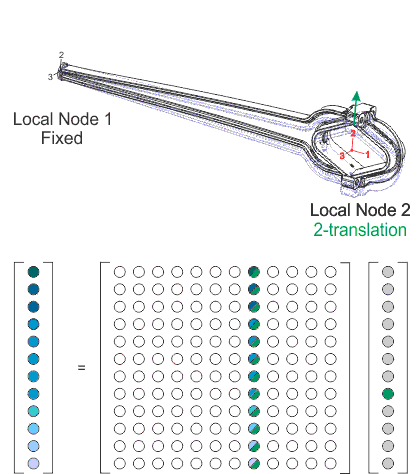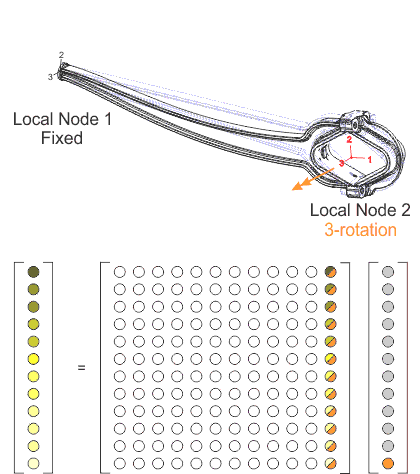
剛性マトリクスは、2つの取り付け点（これらの接続点はコネクタ要素の節点に対応します）で一連の小さい所定の変位を受けることにより、任意の構造から容易に抽出することができます。局所的な自由度における各所定の変位は、12x12の剛性マトリクスに列を与える12の反力およびモーメントを提供します。図5は、構造を調べて剛性マトリクスを追加するプロセスを示します。

完全なコネクタ要素モデル

図6はこのページのトップに示されている3Dソリッドモデルと同じ時間依存の負荷を受けるアセンブリのコネクタ要素モデルを示しています。図7は、時間依存の負荷と同じ力に対する各モデルによって予測された応答を示します。

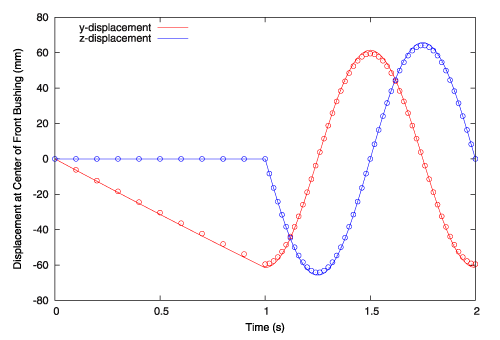
サスペンションが関節運動し、部品が（リアブッシュが曲がるときのように）有限の回転を受けると、コネクタ要素 のローカル座標系が要素に追従し、応答が適切に変換されます。ご覧頂けるように、実質的に同じ結果が得られますが、コネクタ要素モデルは、はるかに計算上効率的であることは明らかです。

結論

この例は、線形または非線形の弾性挙動のモデリングにコネクタ要素を使用する方法を示しています。 また、線形または非線形の減衰挙動をモデル化するために、コネクタ要素を使用することもできます。 例えば、コイルオーバーショックアセンブリは、剛性応答と減衰応答の両方を有する単一の非線形コネクタ要素 を使用して容易にモデル化することができます。 ユーザは減衰マトリクスを直接指定することもできます。

コネクター要素は、ADINAの高度な非線形機能に加えられた最新のものであり、一般的な定式化と柔軟性により、ユーザーはパワフルで効率的なモデリング技術に簡単にアクセスできます。

<< ADINAショーケース 2014から現在 の一覧に戻る